1. Pengertian
Bangun Ruang
Bangun ruang merupakan sebutan untuk bangun-bangun tiga dimensi atau
1. BALOK
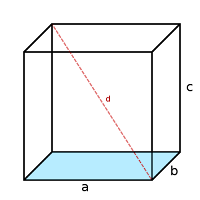
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling tidak satu pasang diantaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut.
Elemen balok :
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling tidak satu pasang diantaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut.
Elemen balok :
- Panjang (p) adalah rusuk terpanjang dari alas balok.
- Lebar (l) adalah rusuk terpendek dari sisi alas balok.
- Tinggi (t) adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.
a. Ciri-ciri Balok :
1. Alasnya berbentuk segi empat
2. Terdiri dari 12 rusuk
3. Mempunyai 6 bidang sisi
4. Memiliki 8 titik sudut
5. Seluruh sudutnya siku-siku
6. Mempunyai 4 diagonal ruang dan 12 diagonal bidang
b. Rumus pada balok
- Luas permukaan
- Volume
- Panjang diagonal ruang
- Panjang diagonal bidang
 |
 |
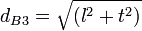 |
Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat.
a.
Ciri - ciri
Kubus :
1. Jumlah bidang sisi ada 6 buah yang berbentuk bujur sangkar (ABCD,
EFGH, ABFE, BCGF, CDHG, ADHE,)
2. Mempunyai 8 titik sudut (A, B, C, D, E, F, G, H)
3. Mempunyai 12 rusuk yang sama panjang (AB, CD, EF, GH, AE, BF,
CG, DH, AD, BC, EH, FG)
4. Semua sudutnya siku-siku
5. Mempunyai 4 diagonal ruang dan 12 diagonal bidang (4 diagonal
ruang = garis AG, BH, CE, DF dan 12 diagonal bidang = garisAC, BD, EG, FH, AH, DE,
BG, CF, AF, BE, CH, DG)
b.Rumus pada kubus
- Luas
 |
- Volume
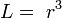 |
Dalam geometri, tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Kubus memiliki 3 sisi dan 2 rusuk.
Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung.
1. Mempunyai 2 rusuk
2. Alas dan atapnya berupa lingkaran
3. Mempunyai 3 bidang sisi ( 2 bidang sisi lingkaran atas dan
bawah, 1 bidang selimut)
b. Rumus tabung:
- Luas alas
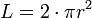 |
- Luas selimut
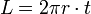 |
- Luas permukaan
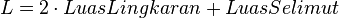 |

- Volume
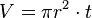 |
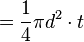 |
Dalam geometri, limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga.
Kerucut dapat disebut sebagai limas dengan alas berbentuk lingkaran.
Limas dengan alas berupa persegi disebut juga piramida.
a.
Ciri-ciri :
1. Alasnya berbentuk segiempat (BCDE)
2. Mempunyai 5 bidang sisi (BCDE, ABC, ACD,ABE, ADE)
3. Mempunyai 5 titik sudut ( A, B,C,D,E)
4. Mempunyai 8 rusuk (AB, AC,AD,AE,BC,CD,DE,BE)
b. Rumus limas segiempat
- Luas permukaan
Luas permukaan limas dengan alas segi-n dapat dihitung dengan rumus berikut:
 |
- Volume
 |
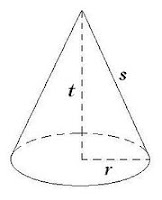
Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.
Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang lengkung yang disebut selimut kerucut.
a.
Ciri-ciri :
1. Mempunyai 2 bidang sisi (1 bidang sisi lingkaran dan 1 bidang
sisi selimut)
2. Mempunyai 2 rusuk dan 1 titik sudut
b. Rumus kerucut:
- Luas alas
L = πr2
- Luas selimut
 |
- Luas permukaan
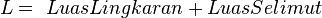 |
 |
Dalam geometri, bola adalah bangun ruang tiga dimensi yang dibentuk oleh tak hingga lingkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya memiliki 1 sisi.

a. Ciri-ciri :
1. Hanya mempunyai 1 bidang
sisi
2.
Tidak mempunyai sudut dan tidak mempunyai rusuk
b. Rumus bola:
- Luas permukaan
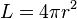 |
- Volume
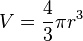 |
Prisma Tegak segitiga siku-siku Adalah prisma yang rusuk tegaknya tegak lurus pada bidang alas. Pada paralelepipedum, ketiga rusuk yang bertemu disebuah titik sudut disebut rusuk-rusuk utama.
a. Ciri-ciri
1. Terdiri dari 6 titik sudut
2. Mempunyai 9 buah rusuk
3 Mempunyai 5 bidang sisi
b. Rumus
Prisma tegak segitiga siku – siku
Ø Luas sisi prisma : jumlah panjang rusuk alas x tinggi + luas 2
tutup
Ø Volume prisma : luas alas x tinggi



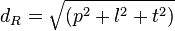





















0 komentar:
Posting Komentar